Many people have asked us about the tides; below are answers to a selection of their questions.
Click on the questions to show/hide the answers. Please note that the usual disclaimer applies to any information given.
Tides are the short term periodic rise and fall of the world’s oceans. They result from the gravitational interaction between the Earth, the moon and to a lesser extent, the sun.
Different parts of the world experience different tidal regimes. Around the UK, there are mostly two high tides and two low tides each day: this is called a semi-diurnal regime. Other parts of the world have a diurnal tidal regime with only one high tide and one low tide each day. The difference in height between high tide and low tide is called the tidal range.
Tides are due to the combined effects of gravitational attraction and the revolution of the Earth-moon system about its common centre of mass. At this point (which lies within the solid Earth) the gravitational attraction between Earth and moon exactly balances the forces required to maintain the moon’s orbit. Elsewhere the two forces are not in balance and give rise to the so-called tide generating force.
The side of the Earth closest to the moon has the strongest gravitational attraction towards the moon while water on the other side of the Earth experiences a weaker gravitational force. A convenient concept is to think of the tide generating forces causing an ovoid of water, aligned with the position of the moon, enveloping the Earth (although this is an over-simplification and such a bulge does not exist in nature). According to this model, there are two bulges of water (high tides) divided by troughs of water (low tides) around the Earth.
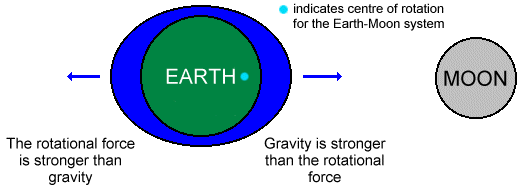
The schematic diagram above depicts the interaction between the Earth and the moon which explains the lunar tides. The gravitational influence of the sun on the Earth’s surface manifests itself in a similar way giving rise to solar tides.
The moon has the dominant effect. The tide generating force is proportional to the product of the mass of the two bodies but also inversely proportional to the cube of the distance between them. The moon therefore has the dominant effect: although its mass is much less than the sun it is far closer to the Earth. The tide generating force due to the sun is 0.46 times that of the moon.
Spring tides occur when the lunar and solar semi-diurnal tides interfere constructively. Using the simplistic analogy of tidal bulges – this is when the lunar tidal bulge and the solar tidal bulge are superimposed upon one another. This occurs when the sun and the moon are aligned in space at either new moon or full moon. Spring high tides are higher and spring low tides are lower than average. Neap tides occur when the moon is at its first or third quarter. Now the lunar tide and solar tide cancel each other out, leading to a smaller tidal range than average. The spring-neap cycle causes tides to build to a maximum and fall to a minimum twice each month.
The regularity of astronomical forcing, combined with the geometry and friction of the real oceans result in spring tides occurring between one to two days after new or full moon. For any specific location, high water at spring tides occurs at approximately the same time of day: for example, at Liverpool spring high tides are always around midday and midnight.
Neap means low. Spring doesn’t have any connotations with the season and the origins of, ‘spring tide’, are not known for certain. One idea is that it comes from the Scandinavian word for ‘leap up’ or that it refers to the natural feature of a spring, a place where water wells up from the ground.
Tides can be predicted far in advance and with a high degree of accuracy. Tides are forced by the orbital relationships between the Earth, the moon and the sun. These relationships are very well understood and the position of the celestial bodies can be forecast very accurately into the future. However, as sea levels rise, the periodicity and range of the tide will be altered due to different bathymetry (underwater depth) and topography (the physical features of an area). Therefore predicting tides a long way into the future could be less accurate. Storm surges are short term sea level changes caused by the weather (winds and atmospheric pressure) that also affect tidal predictability. Storm surges can only be forecast with the same time horizon as weather forecasting (about two to five days).
The predictability of planetary motion means that we can also reconstruct tides in the past. For instance, we know that the disastrous flooding of the Bristol Channel on 30 January 1607 (New Style) occurred at 9am – exactly the time of high water. This, combined with records of high winds, allows us to rule out a tsunami as the cause of the disaster. Tidal knowledge also explains the phases of fighting in the famous Battle of Maldon (10 August 991 New Style): the ebbing tide allowed Vikings to cross a causeway in the River Blackwater in Essex where they then slaughtered the Anglo-Saxon Brythnoth and his men.
No, the tidal force generated by other planets is negligible. The nearest approach of Venus to Earth is more than a hundred times further than the moon. The tidal force is approximately 0.000054 times that of the moon. The next most significant effect is from Jupiter, with a tidal force of 0.000005 times that of the moon. Even if all the planets aligned such that their effects combined the additional force would be insignificant.
In UK waters, high tides occur approximately every 12 hours 25 minutes. It takes 24 hours and 50 minutes (a lunar day) for the same location on Earth to re-align with the moon. This is because the moon orbits the Earth in the same direction that the Earth rotates on its axis. This extra 50 minutes means that the same location will experience high tides every 12 hours 25 minutes. This varies between different locations as the local geography has an effect on tidal dynamics.
No, although most coastal locations in Britain experience two tides a day there are some places which experience what is known as a double-high water (for example, Southampton) or double-low water (for example, Weymouth). Dynamical effects (the mathematics governing water motion) combine with the bathymetry (water depth) to create higher frequency tidal harmonics that interact with the primary tidal forces to create these more complex tides. The tide gauge at Lowestoft displays a mixed semidiurnal tide where the diurnal (daily) tidal constituent is large enough to cause significant changes to the high and low tides every lunar day.
The diagrams below are tidal curves for Liverpool on the west coast, Lowestoft on the east coast and Weymouth on the south coast.
The first tidal curve is from Liverpool where there is a semi-diurnal tidal regime. The second graph is a tidal curve from Lowestoft showing the mixed nature of the tidal range on a daily basis. The third graph shows the tidal regime of Weymouth with complex double low tide behaviour.
As has already been noted, some places around the world have diurnal tides – meaning there is only one high and one low tide a day: Karumba in Queensland, Australia, has a diurnal tidal pattern.
The shape of the coastline and the bathymetry (water depth) result in different tide times around the coast of Britain. Tides travel as waves (moving at about 20ms−1 in shallow seas and at hundreds of ms−1 in the deep ocean). These tidal waves that transverse the oceans are interrupted by land masses. When the tidal wave crosses onto the shelf seas, the wave’s speed decreases and the wave is refracted by the local bathymetry. Also, land masses prevent the tidal wave from moving in a uniform direction. For example, St Mary’s in the Isles of Scilly experiences high tide while at the other end of the south coast, Dover is experiencing low tide. The tidal amplitude around the country also differs widely. The Bristol Channel experiences the third highest global tidal, with a mean spring range of 12.3m, while on the east coast Lowestoft experiences a much reduced mean spring tide range of 1.9m.
The following are the top six mean tidal ranges around the world.
| Location | Mean spring tidal range |
|---|---|
| Bay of Fundy, Nova Scotia | 12.9m |
| Ungava Bay, Quebec, Canada | 12.5m |
| Avonmouth, United Kingdom | 12.3m |
| Granville, France | 11.4m |
| Rio Gallegos, Argentina | 10.4m |
| Cook Inlet, Alaska, USA | 9.2m |
Spring tides are particularly large close to the equinoxes (21 March and 21 September) when the sun is overhead at the equator. Other astronomical factors can cause tides to be larger than average. The tides are slightly greater when the moon is closest to Earth in its orbit, at perigee. The angle of the orbit of the moon to the equator, its declination, is another factor. Additionally, the moon has a ‘nodal cycle’ of 18.6 years.
Maximum diurnal tidal ranges occur when lunar declination is greatest and become smaller when the declination is zero. Solar tides are larger when the sun is in its perihelion position, when Earth is closest to the sun in its elliptical orbit – but this currently occurs on 3 January each year and therefore cannot coincide with the more important effect of the equinoxes.
The tide at any place can be thought of as the sum of a large number of components, called constituents, each of which is associated with a distinct physical (usually astronomical) cause. As long as the periodicity of the constituent is known, its amplitude (size) and timing with respect to other constituents (its phase) can be found by a process called harmonic analysis. The first practical method was put forward by Sir William Thomson (Lord Kelvin) in 1867.
There are several steps involved in creating a tide table. Firstly, a long sequence (or time series) of tidal observations for that port or location are needed. This time series will include all the astronomical effects and the higher harmonics produced by the tidal behaviour in shallow water, as well as noise due to the weather-induced effects (the storm surge). Some examples of the periods of leading astronomical forcings are:
- 12.00-hour cycle for the principal solar constituent (S2)
- 12.43-hour cycle for the principal lunar constituent (M2)
- 27.2122-day cycle caused by change in lunar declination (moon’s angle to the Earth)
- 27.5546-day cycle caused by a regular change in the Earth-moon distance
The process of harmonic analysis gives the amplitudes and phases of all constituents (a routine analysis of one year of tide gauge data will normally identify 120 constituents). These pairs of values (known as harmonic constants) are unique for every location.
The amplitude and phase for each constituent combined with the angular speed of that constituent allows the prediction of its contribution to the overall tide forward or backward in time. Adding up the effects of all the constituents at a given location provides a full tidal prediction. For more details, see the Marine Data Products Team’s Tidal Prediction Service.